Research Article
The Higgs Decays and Cusps
18312
Views & Citations17312
Likes & Shares
In a new evolution after a big bang, coordinate generation and annihilation are discussed, using cross products, projections and fiber bundle maps. As new force color charges, independent of QCD, with rgb-gravitons are related to the octonion G-compass. New measuring Gleason operators as GF are described. Decay geometries for systems are set on dihedrals with nth roots of unity as characteristic polynomials.
DARK MATTER, OCTONIONS AND GF
Dark matter Q is presented in the MINT-Wigris model as a Horn torus with energies inside. If energy is stored as 1-dimensional retracted quark lemniscates Pj, arranged in retracted nucleons as butterflies P with six wings their radius r ‘inversion as decay of the Horn torus is at the Schwarzschild radius Rs of Q where they get in the universe a radius r with r ‘r = Rs. The change of dimension from 1 to 3 space dimensions xyz is due to adding an eigen rotation of the system, called spin. This is by projective duality, using a correlation in a real projective space P5. To a point O as origin of space xyz-coordinates corresponds a 4-dimensional hyperplane as spacetime with xyzt-coordinates. The xy-plane is taken as the aggression disk of Q with origin O. The above radius inversion is at a (radius normed) unit circle U (1) of an octonion 7th Kaluza-Klein rolled coordinate. To a point as barycenter of the universes nucleon P (or Pj) corresponds a common center P ‘of the lemniscates with the above radius inversion. Higgs bosons or field can set a mass scalar as kg-weight at P, P ‘which is an octonion 5th coordinate. If octonion coordinates are listed in tuples of indices, there are at this decay steps 123457 for six octonion coordinates.
Inversion of time 4 to 6 as frequency f = 1/∆t is for speeds v = ∆x/∆t. Dark matter in Q has speed v ‘>c, inverted to universes matter speed to v<c in v ‘v = c.
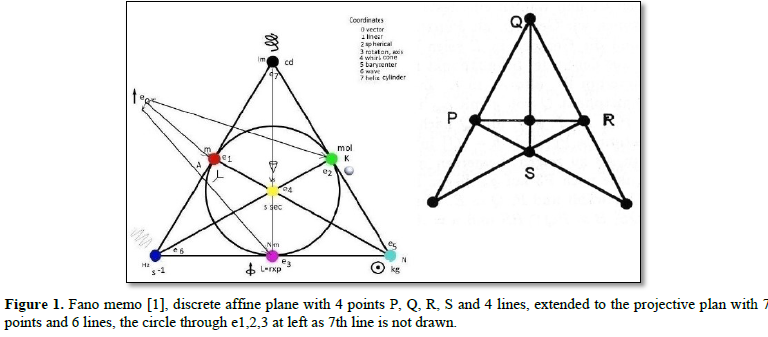
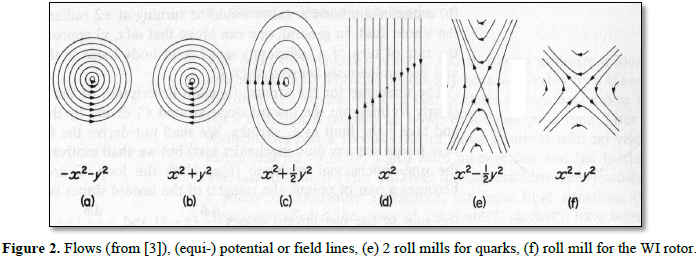
Octonions have in 1234567 seven Pauli matrix extended base triples (lines in Figure 1 with three points as GF triple), Gleason operator frames GF as measuring apparatus, listed in the Fano memo (Figure 1). The spin triple 123 matrices belong also to the weak interactions WI as SU (2) generators. Triples like 123 are measuring operator frames. They have weights attached at their three vectors, for spin as 123 it is length/meter in space. For gravity a SU (3) strong interaction SI triple 126 GF, using GellMann extended Pauli matrices λ1,2,3, is added which makes a space with 7 octonion variables and 3 parameters for three color charges red 1r, green 2g and blue 6b. The octonion coordinate e0 1r (an eigenvector of a matrix G, also for wave length λ or radius r), noted as 0 if no confusion numerical occurs, is obtained by bifurcating 3 into a plane 03. This correlation of a line 3 with a plane 03 is in a 4-dimensional P4 space. The relation with P5 is that to P4 is added a real 5-cell R5. It is for a Higgs field, used in [10] for a Kaluza-Klein projective unification POT (as force and potential) of the electrical EM with the gravity GR potentials EM (pot), E(pot). They are a driving motor for quarks, having a 2-roll mill inner plasma flow about their two foci of the central lemniscate (Figure 2). P5 has as projections 1234 for EM (pot), EM and the weak interaction WI. There are two more projections of P5. 1256 is for E(pot), GR which makes the real 6-, complex 3- dimensional octonion subspace 123456. The third projection is 3456 for CP² as complex 2- dimensional space for nucleons and atomic kernels. It arises as base of a fiber bundle g: S5 → CP² with fiber S1 (U (1) 7). 1234 has the Hopf fiber bundle with fiber U (1) h: S3 → S². These unit spheres Sn in a real space of one dimension higher are topological 1-point ∞ compactifications of a real space Rn with a stereographic map stn: Sn → Rn from ∞ as central projection.
For the rgb-graviton are added to octonions with 1r as orthogonal base vectors the 2g, 6b parameters, generating to R5 as cell of P5 a 5-dimensional complex extended space C5. In projective notation, real (or complex) to P1 ≡ S1 (C1 ≡ S², the unit sphere in R²) are topological added n-cells, n = 2,3,4,5, in form of Xk = Yk U X(k-1), X = P, Y = R (X = CP, Y = C). Octonions and SU (3) correspond to C4 and C4 is extended, by using the complex cross product, to z5 = (2g,6b) = z1 xz2 xz3 xz4. The dark matter Q aggregation disk as octonion 12 xy-plane is after a Higgs decay of Q extended to a complex 2-dimensional space with coordinates 12(2g) (6b). The coordinate 2g is for a phase angle φ0 and exponential function exp(iφ0), adding to waves exp(iωt) with t time and angular frequency ω = 2πf = dφ/dt (f frequency) a phase translation exp(i(ωt+φ0)). The angle as θ on 3 for the angular position of a compass needle 0 occurs also between two rays as in Figure 2 for GR generated orthogonal and spiralic projections. If the rays are in direction of an octonion coordinate ga,b which belongs to two different systems a,b, the measures of their eigenvectors on gj are rescaled by cos φ0 (contracted or extended) when observed on gk, k ≠ j (Figure 3). The third rgb-graviton parameter of z5 6b is for measuring frequency through winding numbers ω = 2πf = dφ/ dt with f = 1/∆t = n, n =1, 2,… natural numbers. The counting comes from the linear universal cover R 7 of S1 as Kaluza-Klein rolled U (1) symmetry of the electromagnetic interaction EMI. In 2π circulations about S1, counted by n through a residual complex S1 contour integration, the EMI frequency has for exp(iωt) the period 2πn which rolls R up to S1; the circulation time is ∆t = 1/n. time inversion to f quantizes time, for instance as a Calderon or the Planck time. As triple (ω,t,f) 346 is a spin-like Gleason operator GF frame as an orthogonal base triple. For 345 can be used 3 in Joule as rotational energy E(rot), 4 as time measured in seconds s or magnetic field strength E(magn) measured in Wb, for 6 measured as inverse time in s-1. For 0 as 1r 037 as (r,θ,exp(iφ)) can serve as a compass 07 extended measuring GF. For 2g a measuring GF triple is 2(2g)7 as (φ, θ,exp(iφ)) 237. θ is a turning spherical angle towards the space z-axis 3. As trifurcations appear 2,3. 2 for heat has the Fano 246 GF, 3 for rotation the Fano 347 GF, but the trifurcations are for 2 as [2, φ0,7] and for 3 [ω,t,f]. The GF ‘s can be extended for quasiparticle presentations.
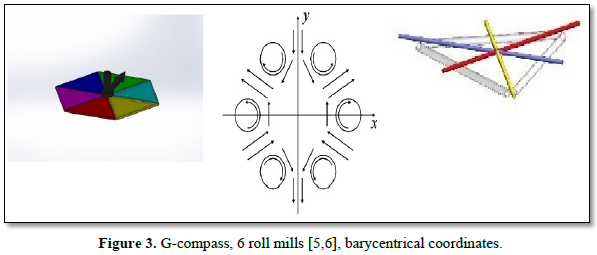
As new force on 0 is suggested the color charge force cc with rgb and conjugates c(r)c(g)c(b) as six G-compass values (Figure 4); the GF triple is 126, the rgb-gravitons; 2 as 2g and 6 as 6b are z5 parameters, not variables. Among the catastrophes, the cusp fits to 126 as (1r) (2g) (6b) with 1r as variable.
The aggregation disks xy-plane Exy is also extended by the octonion 7 coordinate. It was used as linear universal cover of the unit circle U (1) in Exy. Wave length (meter for space) is quantized by spin vector lengths, using the Planck constant h. R is presented as helix line on a cylinder with U (1) as transversal section. There are energies and measuring GF ‘s associated with all octonion coordinates EM (pot) Ampere 1 with 123 GF (also for meter); Kelvin k for 2 E(heat) with GF 246, E(rot) Joule 3 with 346 or 347 GF; E(magn) with GF 145 or time 4 with Wb or s; E(pot) kg 5 with 257 GF; E(kin) as frequency 6 with s-1 and GF 356, and 7 cd EMI with GF 167. An additional strong interactions GF was 126 for GR rgb-gravitons as superposition of three cc whirls for the nucleons neutral color charge. Quarks in nucleons have always r,g,b color charges in gluon exchanges which change the states and locations in nucleons. Counting also 037, 237, 346, there are 11 GF in use, more can be invented for quasiparticles (32 in a list).




In the first line of the Figure 5 are the spherical SI coordinates, possibly 7- (or 8-)dimensional extended with exponential/polar coordinates. In the second line are the linear Pauli/Euclidean coordinates, in the third line a distribution of color charges to the SI coordinates. The fourth (fifth) line contains the D3 (SU (2) Pauli) MTs as cross ratios. Their matrix names are in the sixth line, together with the Einstein matrices. The following line is a numbering for a strong 6-fold integration series (also the Fano figures numbers which are for octonions). The next line contains the Planck numbers. Energy vectors are in the third to last line and the next line contains natural constants and three more operators, C (conjugation for quantum numbers), T (time reversal) and P (space parity) of physics.
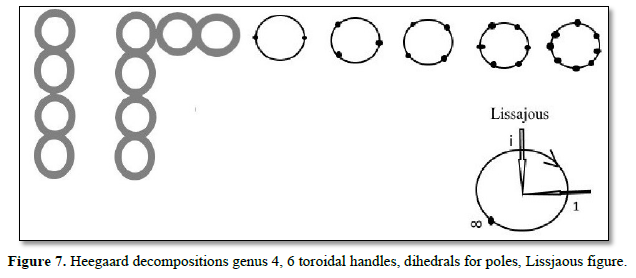
The Figure 5 is from the 1998 book of the author, revised by adding at left and right two columns for the octonion extension 01234567 of the old color charge space 123456, extending spacetime 1234. The first row is introduced for color charges as own energy force E(cc), having as values the complex six cross ratios in line 4 for color charges in line 3. A G-compass for 2x2-matrix extension for octonion coordinates is added at left with an eigenvector eo. All coefficient matrices of complex cross ratios in the 4th line get an eigenvector attached for setting their energy units, listed in 8th line. In the third line of the first column is in the third row listed a turning angle for the G-compass needle ea. It uses the kth roots of unity on exp (1θ) as the G-compass boundary, a unit circle, for discrete turns. To this belong weak decays of the SU (2) geometry S³, its Heegaard decompositions into two solid handle bodies of genus k. Manifolds are bounding them in form of k tori glued at a 2-dimensional sphere S². Drawn on U (1) as k points for a dihedral Dk, the symmetries of order 2k describe dynamical rotors for the basic interactions. As points, k = 1 presents a monopole where an energies charge can be set, k = 2 is for dipoles, magnetic momentum for instance, k = 3 is for the quark triangle of a nucleon, k = 4 (powers of the imaginary number i) is a weak WI rotor and k = 6 is a strong SI rotor. The WI rotor is driven by the weak interaction WI and a unified POT force of the electrical and gravity potentials. To this is added the strong interaction force SI for the SI rotor. This one describes dynamically a quark-gluon plasma inside a nucleon. It is constructed as 6 roll mills in catastrophe theory and has as potential the elliptic umbilic with 2 variables and 3 parameters. The parameter interpretation of the octonion coordinates is used in the table: φ 2 has two parameters as φo in the first row and in exp (i φ) in the last row. The parameters of θ are in the first row and in the last row as angular frequency (speed) = 2πf = dφ/dt, listed as f. Time t has T in the last row as parameter. In the first row is listed a 2x2-matrix G which is the order 6 scaled coefficient matrix of E(rot). It is interpreted as an acoustic or gravitational, spiralic rgb whirl rotation circulation time of a rgb-graviton as superposition of three-color charge whirls r red, g green, b blue, observed as neutral color charge of nucleons. The triples count for 3-dimensional orthogonal base measuring frames GF like spin which measures length in space as meter. In the 8th line are listed the names for energies and their GF triples (last line) are found in the authors 2019 book and in her older publications. An octonion Fano memo exists seven GF, rgb as 126 is added to them.
In the last column, f counts natural numbers n (and 0) for winding numbers about a circle exp (i φ) (in the 5th line). Below is R for the real number plane as universal cover of the U (1) circle (6th line). R winds above U (1) as helix line on a cylinder and 2mm counts its winding numbers as period of exp (i φ). T in the fourth line is the circulation time for n windings. The linear octonian coordinate is 7 (7th line). The measuring force unit is candela cd. The coordinate 7 presents the electromagnetic interaction EMI energy.

Higgs decay, orbits and cusps
For the weak interaction, the Heegaard decompositions of S³ into solid brezels of genus n = 0,1, 2, are for decomposing S³ into two handle bodies of genus n where n = 0 gives two solid balls, with boundary S², splitting S³ at an equator.
The big bang or dark matter Higgs boson decay is different. The xy-plane of it gets extended by the real cross product to the GF 127. The unit circle for 7 (set [x, y,0] in 12) is extended to a cylinder in 127 with axis 7. The exponential function exp(iωt) oscillation is for EMI waves extended to exp(i(ωt+xk+φ0), φ0 a phase angle as parameter, k = 2π/λ wave number, λ wave length as parameter and x substituting for 7 as expansion of the wave on its world line with speed c = v = ∆x/∆t. A projective space extension is [x, y,9 φ0,10 λ]. In the SI GellMann λj matrices λ8 is replaced by λ9, λ10 and their extended GF triples 459, 67(10). If complex extensions of spacetime coordinates z1 = (z,ict), z2 = (x,iy) with the complex cross product to 56 z3 = (m,f) = z1 xz2 is substituted, there are three SI 4-dimensional projection spaces 1234 for WI/EM, 1256 for GR and 3456 for nucleons and atomic kernels as CP², as mentioned before. In complex SI 3x3-matrix extension they are (z1 z2 0), (z1 0 z3), (0 z2 z3).
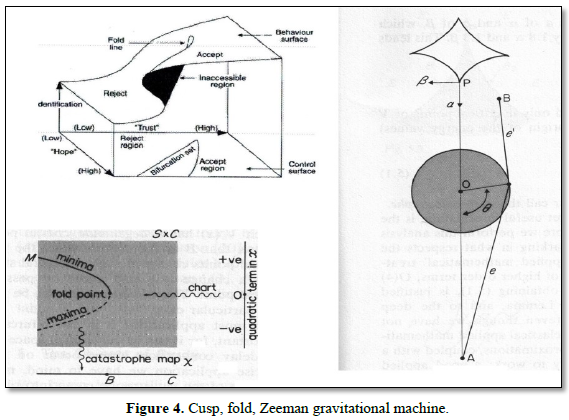
Substituting the [x, y,9,10] coordinates for a cusp catastrophe [3] potential as Vab(x) = x4/4 + ax²/2+bx with the cusp equation u14 + t2u22 + t1u1 and x = u1, y = u2 as variables 9 = t1, 10 = t2 as parameters and x = y for V, the cusp geometry can be used (Figure 4). In the first section, the cusp parameters are interpreted as the rgb-graviton z5 parameters 2g (for 9 and a spherical phase angle θ of the G-compass needles nth roots of unity positions), 6b (for 10 as circulation winding numbers f = n frequencies ω). It means also that in the 127 EMI cylinder above the coordinate 7 is used in projection where for the complex exponential wave function only the real cosine part is observed in spacetime. This is as a finite part for the wave length a cosine oscillation like LASER with two fixed endpoints and one knode O in the middle for cos π = 0. For the radius above inversion [4], a barycenter P ‘is marked on the x-line of Exy and mathematical inverted at a circle with radius √Rs to P. In time P is rotating on the cylinder surface and traces out the exp wave as helix line. The start for P is marked on U (1) as φ0, a phase change. Its image points are connected with P ‘and trace out the rays of the cusp with endpoints P ‘. In the 27 planes of 127 cosine can be interpreted as a cubic equation 4a³ + 27b² = 0 in the control space of V and the fold line (x, -3x²,2x³) in the catastrophe manifold M which in a plane can be substituted for v = u³ replacing cosine, and having at O the uv-planes origin. There are three potential levels (figure 3), one middle unstable part u = 0 containing O, an upper (lower) maximum u<0 (minimum u> 0) potential level for a GF with these 127 three potentials as threshold weights. The Zeeman matching (Figure 4) for GR cusp jumps of a wheel show a superposition of four hyperbolic umbilic catastrophes with potential (two variables and three parameters) Vabc = x³ + y³ +axy + bx +cy.
For the Higgs decay the thresholds mean in the control space that V gets as in the weak decay of S³ a bifurcation into two parts with an upper V1 or lower V2 potential level. For a mass system Q in the universe this sets the first cosmic speed v1²/c² = |φG|, the GR potential and v2 = v1∙√2 as second cosmic speed, using Rs of Q. Equipotential surfaces are spheres S² about a barycenter B and field lines for a GR flow or wave in time are rays with initial point B.
The S² is whirl like rotated in time as a rgb-graviton action. In reduced coordinate form of S1 as a transversal section E of a Minowski double cone (belonging for instance to a parabolic umbilic catastrophe), for a system P orbiting about Q with speed v = v1 it means that the xy-plane E with x² + y² =1 as P orbit is turned in an angle β by the rgb-graviton whirl to a leaning transversal plane Eβ towards the cone M such that the diagonal of an ellipse for the P orbit has a nearest point on M. It moves after one rotation on a small circle in Eβ with the other endpoint of the diagonal on an opposite cone line on a large circle (Figure 4). The P speed-accelerating periodic φ0 2g, phase changing angle is due to the Schwarzschild metric for Q. A similar angle β for the other two Einstein EMI waves changes brakes mirror like the world line of the light ray. This is due to the fact that the speed c can be not accelerated.
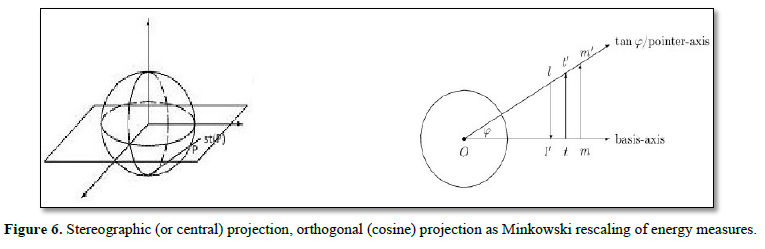
In changing to another direction for its world line, it can emit or absorb energy in relation to mass systems for the double lensing or redshift or when hitting matter surfaces or (potential) energy fields. For a planet rotating about a central sun Q having a common barycenter of the system inside Q it means that increasing the P speed changes β until the diagonal of the ellipse is threshold annihilated and is on the cone surface (parabola orbit of P for escape), turning β further gives hyperbola escape orbits for P. In both cases, there is no common barycenter for P, Q set by Higgs. In case of two galaxies where Higgs sets in relation to their speeds a common barycenter, rgb- gravitons make a spiralic contraction where cos β is used as orthogonal projection from one spiralic ray to an adjacent ray in this angle. This introduces also for a Hilbert space H presentation of 1234 the splitting of H into two orthogonal subspaces H = U + U┴ where a vector u can be written as u = v + w, vεU, wεU┴. Complex vectors z split into z = x +iy = r∙exp(iφ) in polar coordinates with x = r∙cos φ, y = r∙sin φ.
In case several mass systems such as three quarks in a nucleon uud or ddu have a common nucleon barycenter where Higgs sets a nucleon mass, there is a pendulum contraction/expansion by rgb-gravitons of the quark triangle in proportion of the three normed basic spin values ½;1:2. This belongs to an SI rotor [1]. The quark speeds for rotation are between the cosmic speeds belonging to the nucleon barycenter B, B is the intersection of three quark-triangles, conic rotational generated barycentrically coordinates (figure 3) and the quarks barycenter’s are on a circle about B at the triangle’s vertices.
If for matter waves the above wave equation constants are Schroedinger substituted for a common group speed v of the nucleon wave package, this requires that the sum of the quark mass m0 is GF added for the nucleon mass m = mf + mi, set by Higgs at B, with two other GF weights where mf comes from inner transformed frequencies (speeds) in mfc² = hf, h the Planck constant and mi is coming froma special relativistic v rescaling of mass. The m0 mass is about 10 percent of m.
Sudden changes, jumps, tresholds and symmetries
In the former sections, often discrete state changes occur.
The first one was radius inversion when a Higgs boson is decaying its inner dark matter to universes matter. The fold catastrophe has two potential levels for this and a potential function Va = x3/3 +ax. The catastrophe manifold has the equation x² + a = 0 for a parabola (figure 4) with a bifurcation singular point at (0,0) in a xy-plane. For two states the quadratic term V has a maximum for x<0 (lower branch of the parabola) and a minimum for x> 0 (upper branch of the parabola). At (0,0) the threshold value for V sets the bifurcating radius inversion from upper to lower or lower to upper parabola curves. This makes a Higgs boson or black hole Q decay (or dimensional matter collapse). Involved is a correlation in P5.
A SI parametrized cusp space [x, y, φ0,6b] is extending the aggregation xy-plane R² of Q to a 4-dimensional real R4 or projective 3-dimensional P³. For central projective projections like st: S² →R² which is also used for raytracing the P3 presentation is used. For parallels in a Euclidean space Rn, it means that they are closed at infinity by one singular, perspective added point at projective infinity. As example, U (1) is projected down to the octonion 7 tangent on its south pole from ∞ sitting at its north pole, 2-dimensional S² is similarly projected down to the tangent xy-plane by rotation. From P3 the R³ cell coordinates are used. Interpreted is st as a central projection, having a parameter t and constant a as length on a vertical z-axis. If the central projection with coordinates (0,0, a) maps a space point (x,y,z) with coordinate z<a down to the xy-plane, the image has projective coordinates [-ax, 0,z-a]. This applies also to st1 (or st2) which maps S1 down to [x,0,1-z].
The projective norming is [1,0,(z-1)/x]. Using substitutions and scaling, the last coordinate is (z-1)/z or (r-Rs)/r, the Moebius transformation for rotations or the Schwarzschild factor. The coefficient matrix G is of order 6 for the G-compass and color charge force on the octonian e0 coordinate. It has as units setting eigenvector (-p2 ,1), p2 a complex third root of unity. A translation transformation can be for [x,1, z] →[x,0,1-z] with first row (-1 0 0), second row (0 0 0) and third row (0 -1 1).
Consider now the option R4 for (x,y,φ0,6b). Fiber bundles are other projections. SU (2): S³ as unit sphere in R4 has the Hopf projection onto S² as fiber bundle map with fiber S1. Extended SU (3): its S5 has S1 as fiber for its fiber bundle with base CP². If a higher dimensional twisted bundle is invented, S9 in a complex C5 space maps down to S5 as topological factor of the SU (3) geometry. Its fiber is S³ replacing S1. The toroidal S³xS5 geometry of SU (3) replaces the torus in S³ for leptons charge location. A latitude circle in S² has its points blown up by S1 to a 45-degree leaning, rotating circle on the torus surface S1 xS1. Fiber bundle maps are added to projective correlations, changing dimensions.
The phase changing angle φ0 2g from above was used in [1] by the parity operator P for setting an angle β as rescaling factor cos²β for the Minkowski to the Schwarzschild metric. This gives orthogonal, spiralic projections mentioned for 1234 as Hilbert space H, also for Minkowski rescaling with sin φ = v/c, v relativistic speed (Figure 6). With the two cusp parameters as z5 = (φ0,6b) = z1 x z2 x z3 x z4 the real space R5 is extended to the complex space C5. z4 = z1 x z2 xz3 is for the octonions 07, z3 was for mass, frequency (m,f) 56. For real H as R4 the metric is Euclidean <u,u>, for C4 Hermitian. The Minkowski rescaling for spacetime is due to a Morse function M having critical points: to the Euclidean <u,u> metric is applied the time reversal operator T, for instance in reduced u = (r,ct) coordinates to <uT,u> = r² -c²t2 as equation r² = c²t² for the Minkowski light cone. Catastrophes with thresholds (here for the T application), sudden changes, jumps apply also to CPT. As catastrophe thresholds for the setting of T (also C) can be used the fold for T with maximum level for a + sign and counterclockwise rotations mpo, - sign for clockwise cw rotations, also for the change between left- and right-handed space orientations, using base vector determinants. In the Lorentz transformations T changes the sign of the speed between two coordinates as +v or -v. From the CPT operators of physics, the operator C is for complex conjugation and changing all quantum numbers of a quanta system as sudden changes. The CPT symmetry is Z2 x Z2 with C = PT = TP.
P applications are coordinate point rotations u→λu, |λ| = 1, for real, complex or quaternionic u-coordinates. P has associated the cusp catastrophe. The thresholds are also for their sudden changes (Figure 4). Multiplication with λ for P is a coordinate base vector rotation (or point- reflection), a matrix operator using λ. For C as complex z conjugation c(z) the Pauli matrix σ1 generates with the Hopf map application the vector u = (z2 = x +iy,1) to uσ1 (1, c(z2)) tr = z2c(z2) = x² + y² = r² for the complex distance measure. It is also obtained by the reflection (x,iy) →(x,-iy).
Matrix operations as transformations (used for the C operator as σ2 matrix example) are used, replacing catastrophes. The standard models symmetry U(1) xSU(2)xSU(3) is not catastrophe bound [7]. The symmetries set in addition eigenvectors of their matrices as force vectors for energies. For the three forces they come as 1,3,8 symmetry generators of U (1), SU(2), SU(3). GR has the Moebius transformations MT as symmetry of the Riemannina sphere S². The invariants are six cross ratios as matrices for the six color charges. Potential functions fs s-parametrized sets are replaced by exp(iφ) having one variable and one field quantum photon, three WI Pauli matrices for three weak bosons, transmitting energies or acting for decays, 8 SI gluons in a quark-gluon plasma, confining with the gluon exchange between quarks them in nucleons. For EM magnetic field quanta replace the former field quantum’s for electrical charge and potential in 14, 145. For rotations as energy the cc force on e0 can act as symmetry in 03, 037. For 126 as field quantum for GR with mass 5 acts 4-dimensional 1256 as local GR field projection into 1234 about a mass system. U (1) has 7, 167 associated; kinetic energy and momentum p = mv have 6, 356 the SI rotor associated [5]; heat as energy 2 and GF 246 has density of matter in a volume V associates generating pressure on the volumes (spherical) surface. In the last case, the state change of matter between solid, fluid and gas remind again to catastrophes with a triple point and three cusps in superposition, using 126. They appear for instance in the butterfly geometry for 1246 as parameters and one variable 4 added. Two cusps superposition appear in the swallowtail (1 variable, 3 parameters) geometry, an application is for research; it can be for [x, y, φ0, λ]. The case of 4 cusp superpositions appears in figure 3 related to GR. The elliptic umbilic is associated with the 6-roll mill and the SI rotor, for the WI wheel also. The parabolic umbilic (2 variables and 4 parameters) was associated with GR, the swallowtail is contained in it.
Dihedral decays
In the above geometrical considerations, the shapes of decayed systems P are not discussed. In the 9Tool bag are 12 demonstration models and videos for inner dynamics are also available. As a Heegaard decomposition Tool for S³ are here added dihedrals. The WI S³ can decay into two systems like an electron and an antineutrino, coming from the decay of a W- boson. The genus 0 case lets a weak boson decay into two solid, 3-dimensional balls with a bounding sphere S². These can be two copies for two atoms location in spacetime. Hopf spheres for electrons are several copies of S², discrete available as shells using main quantum numbers.
From genus 1 on, the reduced coordinate presentation is by a circle with n = 1,2, 3,.. points in the distance of nth roots of unity marked. They act for 0-dimensional poles carrying an energy or charge. In the 3-dimensional decay blow up for a system P, P has n toroidal handles with a disk Ej removed. A central sphere has n discrete disks removed and at each such boundary is attached an Ej for the P shaped bounding manifold and its homotropy or homology generators. Their higher dimensional generators are not discussed here. In retracts, they are 1-dimensional (Figure 7, Lissajous figures). Beside presentations of equipotential and field lines (Figure 2), the inner dynamics of flows in P is guided by the number of poles, demonstrated as rotating rolls which are driven (for even n) mostly in pairs by a common force as motor. The dihedral D0 is U (1), S1 with no characteristic polynomial for nth roots. The dihedral D1 has genus 1 for a torus and the characteristic polynomial z -1; the conjugation operator for its symmetry of order 2 is for oriented rotations. D2 for POT (electrical, mass/GR potentials) is for quark brezel genus 2 lemniscates with characteristic polynomial z² -1. The inner dynamics of all Dn with characteristic polynomial zn -1 uses finite, cyclic Fibonacci-like difference equation solutions. They replace differential equations. For quarks the 2-roll mill of catastrophe theory applies, the 4-roll mill D4 is for a weak bosonic inner flow rotation, the 6-roll mill D6 as G-compass (figure 3) is for color charges and inner nucleon flows. The nucleons three quarks handle body of genus 3 as D3 is for the SI rotor presentation. The nth roots use often for their finite Fibonacci sequence solutions the powers of eigenvector numbers, belonging to characteristic polynomials. As numbers occur -1 in (-1)n with values {+1.-1}, as p1 or p2, third roots of unity with values {1,p1,p2} or signed as {+1,-1,+p1,-p1 ,+p2 ,-p2} for the 6 roll mill, for n = 4 as {1,i,-1,-i} for the 4 roll mill, also assigned 8th roots of unity. The mills are described in catastrophe theory by potential functions, having 1 or 2 variables and 1-4 parameters.

CONCLUSION
Concerning decays: The Higgs decay makes in the first step the 5-dimensional Higgs field [8]. It can set quarks as energy quantum’s having the two potentials EM (pot), E(pot) unified in the Higgs field. Quarks decay by generating weak bosons and they decay (for instance) in two leptons or two photons. Atomic kernel AK decays arise through the forming of proton-neutron Cooper pairs in AK having an isospin exchange. When the pairs get at too large distance in AK, nuclear decay occurs [9,10]. Concerning sudden changes in systems: catastrophes appear can give thresholds for state changes in systems and state changes are also due to applying symmetry transformation matrices [11-19]. Geometry oriented settings are discussed with models for demonstrations. Dihedrals are one tool for shapes of decay systems. A Tool bag exists which demonstrates many facts for the quanta range.
- Kalmbach GHE (2017) Einstein metrics and two projection maps. MINT-WIGRIS. MINT Verlag, Bad Woerishofen.
- Kalmbach GHE (2020) (Chef-Hrsg) MINT (Mathematik, Informatik, Naturwissenschaften, Technik). MINT Verlag; Bad Woerishofen. pp: 1-65.
- Poston T, Stewart I (1978) Catastrophe theory and its applications. Pitman; London.
- Internet video under YouTube: Moebius Transformations Revealed; 2014.
- Kalmbach GHE, Eberspaecher U (2019) MINT-Wigris Tool Bag; Bad Woerishofen.
- Kalmbach GHE (2020) MINT-Wigris Postulates. In: researchgate.net 2020 under MINT-Wigris Project
- Stierstadt K (1989) Physik der Materie. VCH; Weinheim.
- Schmutzer E (2004) Projektive einheitliche Feldtheorie. Harry Deutsch; Frankfurt.
- MINT-Wigris project (G. Kalmbach H.E.), in the internet under: researchgate.net.
- Kalmbach GHE (2020) A Heisenberg c-compass. J Appl Mater Sci Eng Res 4(2): 63-67.
- Thompson JMT, Hunt GW (1979) A bifurcation theory for the instabilities of optimization and design. In: Berlinski D. (ed.), Mathematical Methods in the Social Sciences.
- Thompson JMT, Gaspar ZA (1977) A buckling model for the set of umbilic catastrophes. (preprint, Eng. Dept. Univ. College, London).
- Thompson JMT, Hunt GW (1973) General Theory of Elastic Stability. Wiley; NewYork.
- Bell GM, Lavis DA (1978) Thermodynamic phase changes and catastrophe theory.
- Stanley HE (1971) Introduction to Phase transitions and critical phenomena. Oxford Univ. Press; London.
- Wald A (1957) On some systems of equations of mathematical economics. Econometrica 19: 368-408.
- Howard IN (1975) Bifurcations in reaction-diffusion problems. Adv Math 16: 246-258.
- Berry MV (1976) Waves and Thom’s theorem. Adv Physics 25: 1-25.










